Cellular Automata
The Cellular Automata series is based on the principles of the Game of Life devised by British mathematician John Horton Conway in 1970, in which a grid of cells evolves over discrete time steps. The living or dead state of each cell in the next generation is determined by its current state and the number of living neighbors it has, according to a set of simple rules. Over time, these rules create complex patterns and behaviors, with cells either dying, surviving, or producing new cells based on their environment.

These rules result in patterns that can stabilize, oscillate, or even grow infinitely, creating a variety of interesting behaviors despite the simplicity of the rules. The game simulates complex systems and is often used to study patterns in mathematics, computer science, and biology.
By transforming these time-based systems into a "frozen" three-dimensional organism, the powerful and magical patterns behind each cellular automaton become visible as a whole. The sculptures seem to have an inner logic and their archaic aspect is reminiscent of mysterious objects from a bygone civilization.
LoaFlipFlop
Period15 Oscillator, welded 12mm carbon steel sheets. Dimensions: 47 cm x 47 cm x 18 cm, 2025.
Download a complete set of photos of LoaFlipFlop HERE.

Loaflipflop is a period-15 oscilator found by Robert Wainwright in 1990.


Loaflipflop in the Game of Life

4GliderSynthesisPentadecathlon
4GliderSynthesisPentadecathlon, welded 12mm carbon steel sheets. Dimensions: 23 cm x 18 cm x 47 cm, 2025.
Download a complete set of photos of 4GliderSynthesisPentadecathlon HERE.
Four glider synthesis visualized in "Life Viewer"
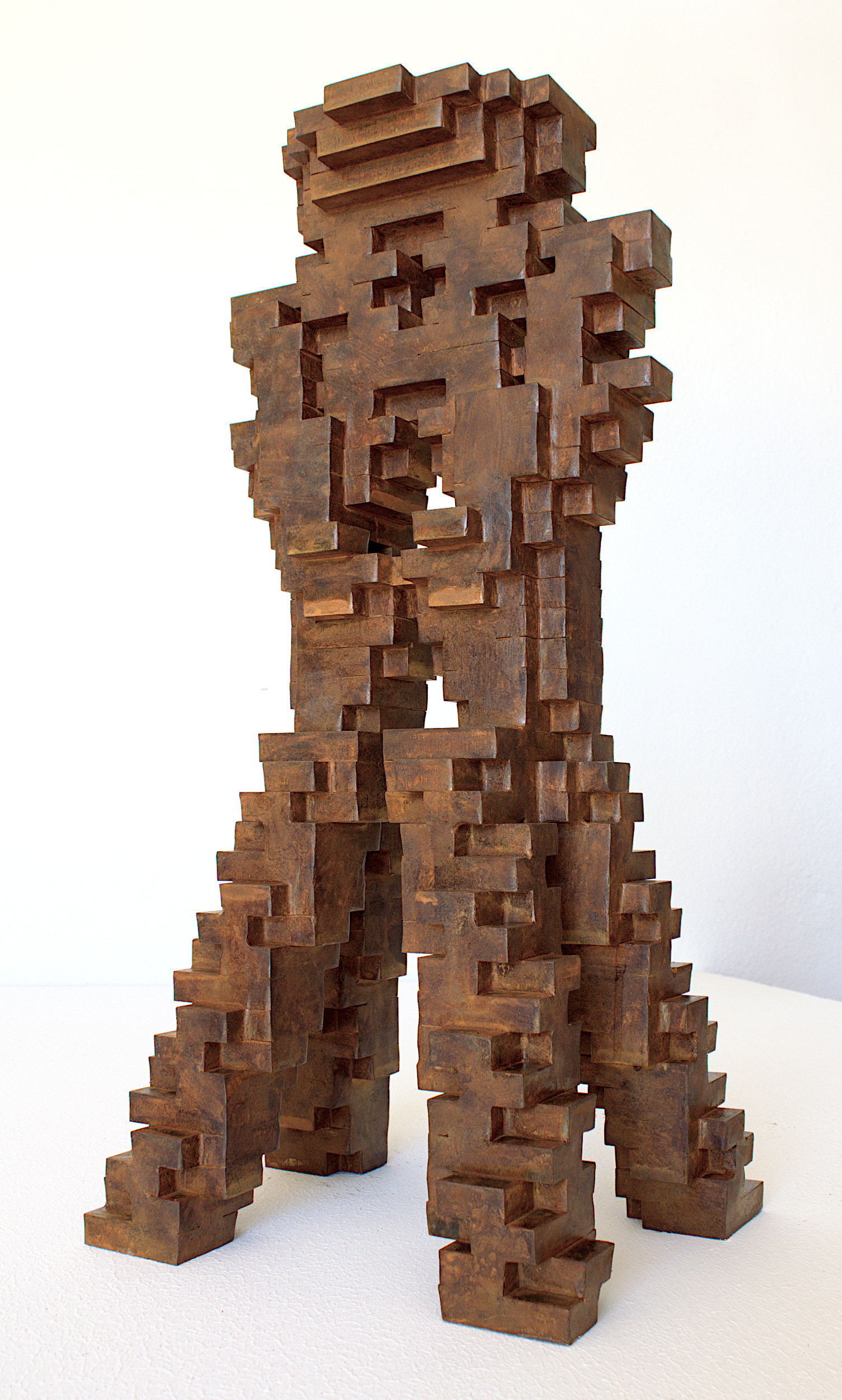
The four glider synthesis into a pentadecathlon oscilator was found by Peter Raynham in 1973.


Technical aspects:
In order to transform the Cellular Automatas into sculptures, two modifications were made:
You can see the difference in the render above: on the right is the original pixel size, on the left is the modified pixel size.